How To Use Prime Factorization To Find Lcm

two.10: Prime Factorization and the To the lowest degree Mutual Multiple (Part 2)

Last updated
Save every bit PDF

Folio ID: 5963

Find the Least Common Multiple (LCM) of Ii Numbers

One of the reasons we await at multiples and primes is to use these techniques to find the least common multiple of two numbers. This will be useful when we add together and decrease fractions with different denominators.

Listing Multiples Method

A common multiple of two numbers is a number that is a multiple of both numbers. Suppose we want to find common multiples of ten and 25. We tin list the start several multiples of each number. Then we wait for multiples that are common to both lists—these are the common multiples.

\[\begin{split} x & \colon \; 10, 20, 30, twoscore, \textbf{50}, lx, 70, 80, 90, \textbf{100}, 110, \ldots \\ 25 & \colon \; 25, \textbf{50}, 75, \textbf{100}, 125, \ldots \end{divide} \nonumber \]

We see that $fifty$ and $100$ announced in both lists. They are common multiples of $x$ and $25$. We would find more common multiples if we connected the list of multiples for each.

The smallest number that is a multiple of ii numbers is called the least common multiple (LCM). And then the least LCM of $10$ and $25$ is $50$.

HOW TO: FIND THE Least Common MULTIPLE (LCM) OF TWO NUMBERS BY LISTING MULTIPLES

Step 1. List the first several multiples of each number.

Pace 2. Look for multiples mutual to both lists. If there are no common multiples in the lists, write out boosted multiples for each number.

Footstep iii. Look for the smallest number that is common to both lists.

Step 4. This number is the LCM.

Example $\PageIndex{v}$: lcm

Find the LCM of $15$ and $xx$ past listing multiples.

Solution

List the first several multiples of $fifteen$ and of $twenty$. Identify the first common multiple.

\[\begin{split}15 & \colon \; 15, 30, 45, \textbf{sixty}, 75, 90, 105, 120 \\ 20 & \colon \; 20, forty, \textbf{60}, 80, 100, 120, 140, 160 \cease{carve up} \nonumber\]

The smallest number to appear on both lists is $60$, so $60$ is the least common multiple of $fifteen$ and $twenty$. Detect that $120$ is on both lists, besides. It is a mutual multiple, but information technology is non the least mutual multiple.

Do $\PageIndex{9}$

Notice the least mutual multiple (LCM) of the given numbers: $nine$ and $12$

Reply: $36$

Exercise $\PageIndex{x}$

Detect the least common multiple (LCM) of the given numbers: $18$ and $24$

Respond: $72$

Prime Factors Method

Another way to observe the least common multiple of two numbers is to employ their prime factors. We'll use this method to find the LCM of $12$ and $18$.

We get-go by finding the prime factorization of each number.

\[12 = 2 \cdot 2 \cdot iii \qquad \qquad 18 = 2 \cdot three \cdot 3 \nonumber\]

And so we write each number as a product of primes, matching primes vertically when possible.

\[\begin{split} 12 & = 2 \cdot 2 \cdot 3 \\ xviii & = 2 \cdot \quad \; 3 \cdot 3 \end{split} \nonumber \]

Now we bring down the primes in each column. The LCM is the product of these factors.

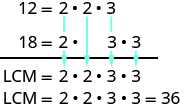
$The image shows the prime factorization of 12 written as the equation 12 equals 2 times 2 times 3. Below this equation is another showing the prime factorization of 18 written as the equation 18 equals 2 times 3 times 3. The two equations line up vertically at the equal symbol. The first 2 in the prime factorization of 12 aligns with the 2 in the prime factorization of 18. Under the second 2 in the prime factorization of 12 is a gap in the prime factorization of 18. Under the 3 in the prime factorization of 12 is the first 3 in the prime factorization of 18. The second 3 in the prime factorization has no factors above it from the prime factorization of 12. A horizontal line is drawn under the prime factorization of 18. Below this line is the equation LCM equal to 2 times 2 times 3 times 3. Arrows are drawn down vertically from the prime factorization of 12 through the prime factorization of 18 ending at the LCM equation. The first arrow starts at the first 2 in the prime factorization of 12 and continues down through the 2 in the prime factorization of 18. Ending with the first 2 in the LCM. The second arrow starts at the next 2 in the prime factorization of 12 and continues down through the gap in the prime factorization of 18. Ending with the second 2 in the LCM. The third arrow starts at the 3 in the prime factorization of 12 and continues down through the first 3 in the prime factorization of 18. Ending with the first 3 in the LCM. The last arrow starts at the second 3 in the prime factorization of 18 and points down to the second 3 in the LCM.$

Notice that the prime factors of $12$ and the prime factors of $xviii$ are included in the LCM. By matching up the common primes, each common prime factor is used only once. This ensures that $36$ is the to the lowest degree common multiple.

HOW TO: Observe THE LCM USING THE Prime number FACTORS METHOD

Step i. Find the prime factorization of each number.

Step 2. Write each number equally a product of primes, matching primes vertically when possible.

Step three. Bring down the primes in each column.

Footstep 4. Multiply the factors to get the LCM.

Example $\PageIndex{6}$: lcm

Find the LCM of $15$ and $18$ using the prime factors method.

Solution

Write each number as a production of primes.	$fifteen = 3 \cdot 5 \qquad \qquad 18 = ii \cdot 3 \cdot 3$
Write each number as a product of primes, matching primes vertically when possible.	$\brainstorm{carve up} 15 & = \quad \; 3 \cdot \qquad 5 \\ eighteen & = 2 \cdot 3 \cdot 3 \end{split}$
Bring down the primes in each column.	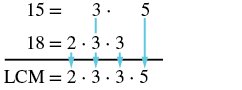$CNX_BMath_Figure_02_05_026_img-03.png$
Multiply the factors to go the LCM.	LCM = 2 • three • iii • 5 The LCM of 15 and xviii is xc.

Do $\PageIndex{11}$

Find the LCM using the prime factors method: $fifteen$ and $20$

Respond: $60$

Exercise $\PageIndex{12}$

Find the LCM using the prime factors method: $fifteen$ and $35$

Reply: $105$

Example $\PageIndex{7}$: lcm

Notice the LCM of $50$ and $100$ using the prime factors method.

Solution

Write the prime factorization of each number.	$fifty = 2 \cdot five \cdot 5 \qquad 100 = 2 \cdot two \cdot 5 \cdot five$
Write each number as a production of primes, matching primes vertically when possible.	$\brainstorm{split} 50 & = \quad \; 2 \cdot five \cdot five \\ 100 & = 2 \cdot 2 \cdot 5 \cdot 5 \stop{dissever}$
Bring downward the primes in each column.	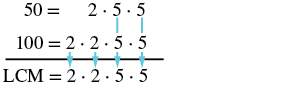$CNX_BMath_Figure_02_05_027_img-03.png$
Multiply the factors to go the LCM.	LCM = 2 • 2 • five • 5 The LCM of l and 100 is 100.

Do $\PageIndex{thirteen}$

Discover the LCM using the prime number factors method: $55, 88$

Answer: $440$

Exercise $\PageIndex{14}$

Find the LCM using the prime factors method: $lx, 72$

Reply: $360$

Central Concepts

Find the prime factorization of a composite number using the tree method.
- Find whatsoever gene pair of the given number, and use these numbers to create ii branches.
- If a factor is prime, that co-operative is complete. Circumvolve the prime.
- If a factor is not prime, write it equally the product of a cistron pair and keep the process.
- Write the composite number as the product of all the circled primes.
Observe the prime factorization of a composite number using the ladder method.
- Divide the number by the smallest prime.
- Continue dividing past that prime until it no longer divides evenly.
- Split by the next prime until it no longer divides evenly.
- Continue until the quotient is a prime.
- Write the composite number as the product of all the primes on the sides and height of the ladder.
Find the LCM by listing multiples.
- Listing the first several multiples of each number.
- Look for multiples common to both lists. If in that location are no mutual multiples in the lists, write out additional multiples for each number.
- Await for the smallest number that is mutual to both lists.
- This number is the LCM.
Find the LCM using the prime factors method.
- Find the prime factorization of each number.
- Write each number as a product of primes, matching primes vertically when possible.
- Bring down the primes in each column.
- Multiply the factors to become the LCM.

Glossary

least common multiple: The smallest number that is a multiple of two numbers is called the least common multiple (LCM).
prime factorization: The prime factorization of a number is the product of prime numbers that equals the number.

Practise Makes Perfect

Find the Prime Factorization of a Composite Number

In the following exercises, find the prime factorization of each number using the factor tree method.

86
78
132
455
693
420
115
225
2475
1560

In the following exercises, find the prime factorization of each number using the ladder method.

56
72
168
252
391
400
432
627
2160
2520

In the following exercises, find the prime factorization of each number using any method.

Find the Least Common Multiple (LCM) of 2 Numbers

In the post-obit exercises, find the least common multiple (LCM) past listing multiples.

8, 12
4, 3
half-dozen, 15
12, xvi
30, twoscore
xx, 30
sixty, 75
44, 55

In the following exercises, detect the least common multiple (LCM) past using the prime number factors method.

eight, 12
12, 16
24, xxx
28, 40
lxx, 84
84, 90

In the following exercises, find the least common multiple (LCM) using whatsoever method.

6, 21
ix, 15
24, 30
32, xl

Everyday Math

Grocery shopping Hot dogs are sold in packages of 10, just hot dog buns come up in packs of eight. What is the smallest number of hot dogs and buns that can be purchased if yous want to accept the same number of hot dogs and buns? (Hint: it is the LCM!)
Grocery shopping Newspaper plates are sold in packages of 12 and political party cups come in packs of 8. What is the smallest number of plates and cups you lot can purchase if yous want to have the aforementioned number of each? (Hint: it is the LCM!)

Writing Exercises

Do you prefer to find the prime factorization of a composite number by using the factor tree method or the ladder method? Why?
Do y'all prefer to find the LCM past list multiples or by using the prime factors method? Why?

Cocky Check

(a) After completing the exercises, utilize this checklist to evaluate your mastery of the objectives of this section.

$CNX_BMath_Figure_AppB_012.jpg$

(b) Overall, after looking at the checklist, practice y'all think you are well-prepared for the side by side Chapter? Why or why not?

Contributors and Attributions

Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Artistic Commons Attribution License 4.0 license.