| When y'all worked with systems of equations, you saw that two coplanar lines
(in the same plane) tin can be arranged in three different situations. Coincide (Coincident)
Lines that coincide lie ane on meridian of the other. They are the Same line with the equations expressed in different forms. If two coincident lines form a system, every point on the line is a solution to the organisation. 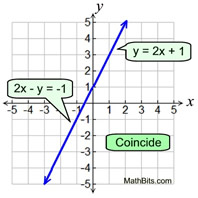 | Parallel
Lines in a plane that are parallel, do not intersect. Ii lines are parallel if they have the same slope, or if they are vertical. If ii parallel lines form a system, there are no solutions to the system. 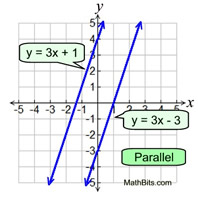 | Intersect
If lines intersect, the lines cross in one point. The angles at which the two lines intersect tin vary. An intersection point creating a 90º angle forms a perpendicular. If two intersecting lines grade a arrangement, at that place is i solution.
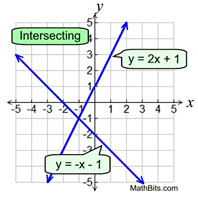 | When we work in 3 dimensions, we will add together another state of affairs to our investigation of lines.
Skew lines are lines that are non coplanar, do not intersect, and are not parallel.
Skew lines exist only in iii or more dimensions. 
Permit's start our investigation of lines past examining parallel lines. |  | Parallel lines are coplanar lines (in the aforementioned aeroplane) that never intersect (never cantankerous each other). | The slope of a line measures its steepness (or its bending from the horizontal).
Lines that are parallel accept the same steepness (or the aforementioned bending from the horizontal).
Since parallel lines have the same steepness, they have the same slope.
Non-vertical parallel lines take the aforementioned slopes!
The slopes are equal. Why did nosotros specify " not-vertical " parallel lines?
In the coordinate plane, all vertical lines are parallel to the y-axis, and are parallel to i another. But, the slopes of vertical lines are undefined since vertical lines have no "run". A "run" of aught causes the "rise/run" fraction to have a zero denominator. When discussing numerical slopes, we cannot mathematically say that an "undefined" gradient equals (or is the same every bit) another "undefined" slope. | Parallel lines are marked with "feathers" (like to what you encounter on an archery arrow) to bear witness that they are parallel. The "feathers" look like "greater than" symbols on the lines. 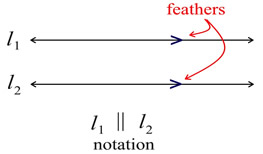 |  | | Equations of Lines:
y = 2 x + 1
y = ii x - v
y = two 10 + i.3
y = 2 10 |  | All of the lines at the left are parallel.
They all have the same slope ( m ).
(y = mx + b) | 
Proving Slope Criteria for Parallel Lines:
Let's prove that parallel lines have equal slopes, AND that equal slopes imply parallel lines. We will look at a "Geometric Proof" and at an "Algebraic Proof". |  | If two singled-out lines are parallel, the slopes of the lines are equal. | Vertical lines will not be considered since their slopes are undefined and cannot be considered equal. If the lines are parallel horizontal lines, the slopes are both zilch. Now let's consider all lines that are not vertical and not horizontal.
Given: Two distinct parallel lines 1000 and n. Prove: The slope of m = the slope of n We will exist cartoon auxiliary lines and constructions to complete this proof. | 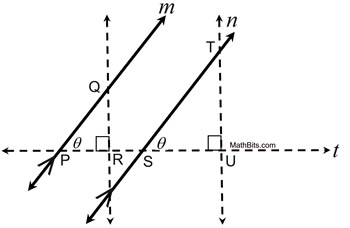 | | | Reasons | | 1. 1000 || north | 1. Given | | two. Draw a transversal line, t, intersecting
at P and S. | 2. Ii points make up one's mind one line. | | three. Construct two perpendiculars to t that
intersect grand at Q and n at T. | 3. From a point not on a line, only 1 perpendicular may be synthetic. | | 4. ∠QPR 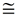 ∠TSU ∠TSU | iv. If two lines are ||, the corresponding angles are coinciding. | | 5.∠PRQ, ∠SUT are correct angles | five. Perpendicular lines form rt. angles. | | 6. ∠PRQ 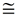 ∠SUT ∠SUT | vi. All right angles are congruent. | | 7. ΔPRQ  ΔSUT ΔSUT | 7. AA for like triangles | | 8. 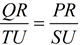 | viii. Corresponding sides of similar triangles are in proportion. | | 9. 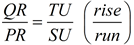 | 9. Property of proportions (alternation). | | 10. slope of m = gradient of northward | 10. Definition of slope (ascent/run). |   | Since we are trying to institute a connectedness between parallel lines and equal slopes, nosotros will need to also prove the antipodal of the theorem stated above. In this manner, nosotros will connect parallel lines to equal slopes AND equal slopes to parallel lines. | |  | If the slopes of two singled-out lines are equal, the lines are parallel. | If the slopes of the lines are both zero, the lines are horizontal and are parallel past definition. Since the slopes of vertical lines are undefined and not considered equal, vertical lines will non be considered.
Given: 2 distinct lines thousand and n with equal slopes. Prove: g || north We will be cartoon auxiliary lines and constructions to complete this proof. | 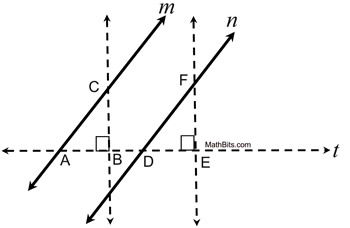 | | | Reasons | | 1. lines m and n with equal slopes | one. Given | | 2. Draw a transversal line, t, intersecting
at A and D. | 2. Two points determine one line. | | 3. Cull bespeak B. Re-create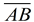 at D, labeling E, at D, labeling E,
such that AB = DE. | 3. A segment may be copied, maintaining its length. | | 4. Construct 2 perpendiculars to t at B and E. | 4. From a point on a line, only ane perpendicular may be constructed. | | 5. 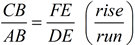 | 5. Definition of slope (rise/run). | | vi. CB • DE = AB • FE | half dozen. In a proportion, product of means equals product of extremes. | | vii. CB • AB = AB • Atomic number 26 | vii. Substitution | | 8. CB = FE | 8. Sectionalization by AB | | 9. 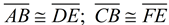 | 9. Congruent segments take = length. | | ten. ΔABC 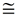 ΔDEF ΔDEF | 10. SAS for coinciding triangles | | 11. ∠BAC 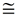 ∠EDF ∠EDF | 11. Corresponding parts of coinciding triangles are congruent. | | 12. m || n | 12. If 2 lines are cutting by a transversal and the corresponding angles are congruent, the lines are parallel. | 
|  | If two distinct lines are parallel, the slopes of the lines are equal. | Vertical lines will non be considered since their undefined slopes cannot be equal.
| We are given that p || q. We can write a linear equation to represent each line.
For line p, y = m ane x + b 1, and for line q, y = thou 2 x + b 2. If lines are parallel, they share no common points. Nosotros saw this when we worked with systems of equations. Parallel systems had no solutions. And so if nosotros set these 2 equations equal, and try to solve for x, in that location must be no solution. Allow's see what happens: | 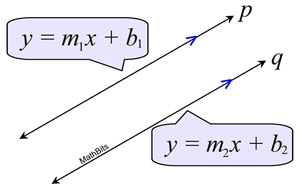 | | m 1 10 + b one = m 2 x + b 2 m 1 x - m 2 x = b 2 - b 1 x(m 1 - m 2) = b 2 - b 1
The simply way there can exist no solution for 10 is for yard 1 - k 2 to equal nix.
thou i - yard 2 = 0
This gives us g 1 = one thousand 2 and the slopes are equal. |   | As was washed in the Geometric Proof, we need to too prove the converse of the theorem. In this manner, nosotros will connect parallel lines to equal slopes AND equal slopes to parallel lines. | |  | If the slopes of two singled-out lines are equal, the lines are parallel. | If the slopes of the lines are both zero, the lines are horizontal and are parallel by definition. Since the slopes of vertical lines are undefined and not considered equal, vertical lines will not be considered.
| We are given that m 1 = m 2. Nosotros can write a linear equation to represent each line.
For line p, y = thousand ane x + b ane, and for line q, y = chiliad 2 x + b 2. If p and q are distinct (different) lines, they will non coincide (be the same line). This means that b one cannot be the same every bit b 2 considering if they are, the lines will exist the exact same line. So nosotros know b ane does not equal b ii. | 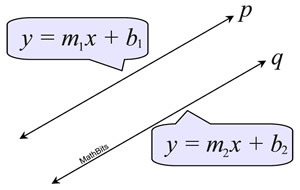 | If lines are parallel, they share no mutual points. We saw this when we worked with systems of equations. Parallel systems had no solutions. So if we set these two equations equal, and try to solve for ten, there must exist no solution. Let'southward run into what happens: k 1 x + b 1 = m 2 ten + b 2 thou 1 x - yard 2 x = b 2 - b one ten(chiliad 1 - g 2) = b ii - b 1
Since we are given that m 1 = m 2 , we know one thousand 1 - g 2 = 0.
ten(0) = b 2 - b 1 b 2 = b 1 Simply, if b 2 = b 1, the ii lines coincide (are the same line).
This is a contradiction to the given that the lines are two distinct lines.
So there is no solution to this system of equations. The lines p and q must exist parallel. |  Annotation: The re-posting of materials (in role or whole) from this site to the Internet is copyright violation
and is non considered "fair use" for educators. Please read the "Terms of Utilise". |












0 Response to "Parallel Lines Have Same Slope"
Post a Comment