Y Mx B X Intercept
How to Notice and Graph ten and y Axis Intercepts Video Lesson
How to Observe x and y axis intercepts
To find an x intercept, substitute y = 0 into the equation and solve for x.
To detect the y centrality intercept, substitute 10 = 0 into the equation and solve for y.
For case, observe the π₯ and y intercepts of 2y + threeπ₯ = 12.
To find the π₯-axis intercept, beginning substitute y = 0 into the equation.
When y = 0, the equation 2y + iiiπ₯ = 12 becomes iiiπ₯ = 12.
Solve the resulting equation for π₯.
3π₯ = 12 can exist solved for π₯ past dividing both sides of the equation by 3.
π₯ = 4 and and then, the π₯-axis intercept has coordinates (4, 0).
To find the y-axis intercept, first substitute π₯ = 0 into the equation.
When π₯ = 0, the equation 2y + 3π₯ = 12 becomes 2y = 12.
Solve the resulting equation for y.
2y = 12 can be solved for y by dividing both sides of the equation by 2.
y = half dozen then, the y-centrality intercept has coordinates (0, half-dozen)
What are π₯ and y Intercepts
The π₯ intercept is the coordinate where a graph touches or crosses through the π₯-axis. It has a y coordinate of 0. The y intercept is the coordinate where a graph touches or crosses the y-axis. Information technology has an π₯ coordinate of 0.
The y-centrality is the vertical axis that passes through the centre of the cartesian axes from bottom to top. It is marked with numbers known equally y coordinates.
The π₯-axis is the horizontal axis that passes through the centre of the cartesian axes from left to right. It is marked with numbers known as π₯ coordinates.
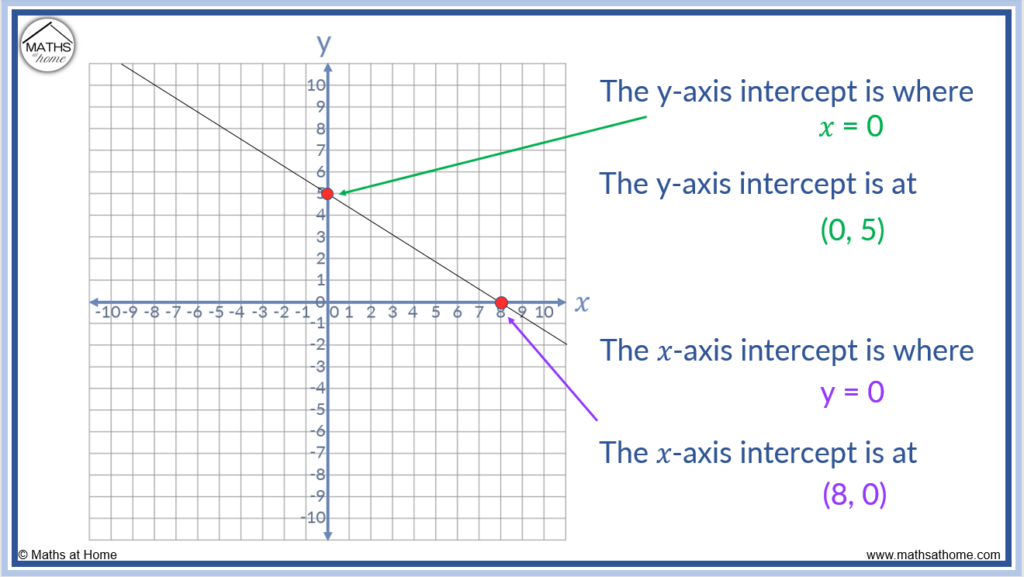
The y-centrality intercept ever has an π₯ coordinate of 0. In the example shown to a higher place, the y intercept is (0, 5) because it passes through the y-axis at y = v.
The π₯-axis intercept always has a y coordinate of 0. In the example shown above, the π₯ intercept is (8, 0) considering information technology passes through the π₯-axis at π₯ = viii.
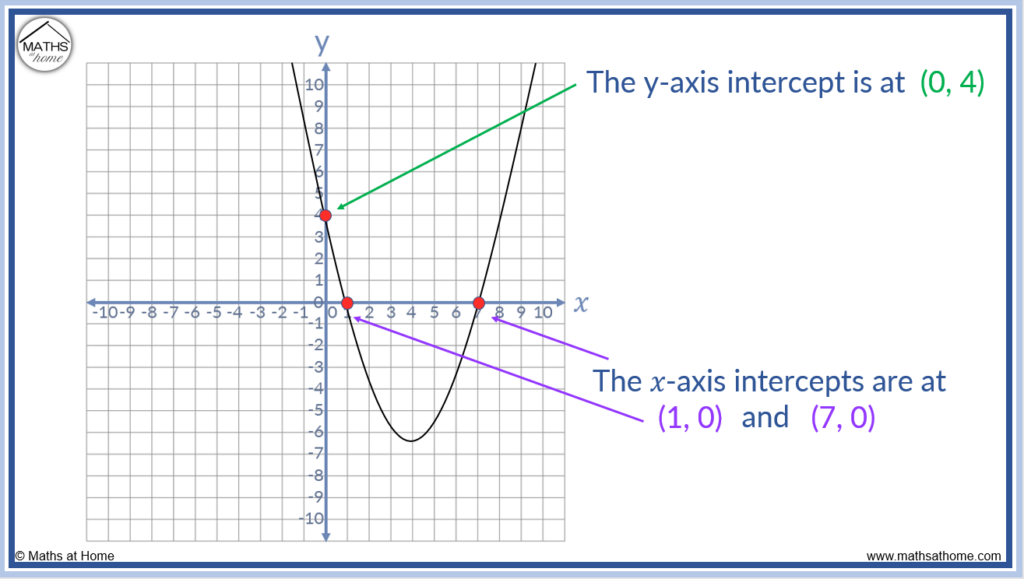
A office can only have ane y-centrality intercept. This is because a function can only have at most ane output for any given input. When π₯ = 0, a function tin simply have ane output which is the y intercept value. The number of π₯-axis intercepts depends on the type of equation.
For instance, in the quadratic equation shown above, there is only one y intercept at (0, four), still, at that place are two π₯ intercepts plant at (i, 0) and (vii, 0). There are two π₯-centrality intercepts in a quadratic equation.
A relation can have an space number of π₯ or y intercepts depending on the equation of the relation. For example, a circle equation can accept 0, 1 or upwards to two π₯-axis and y-axis intercepts.
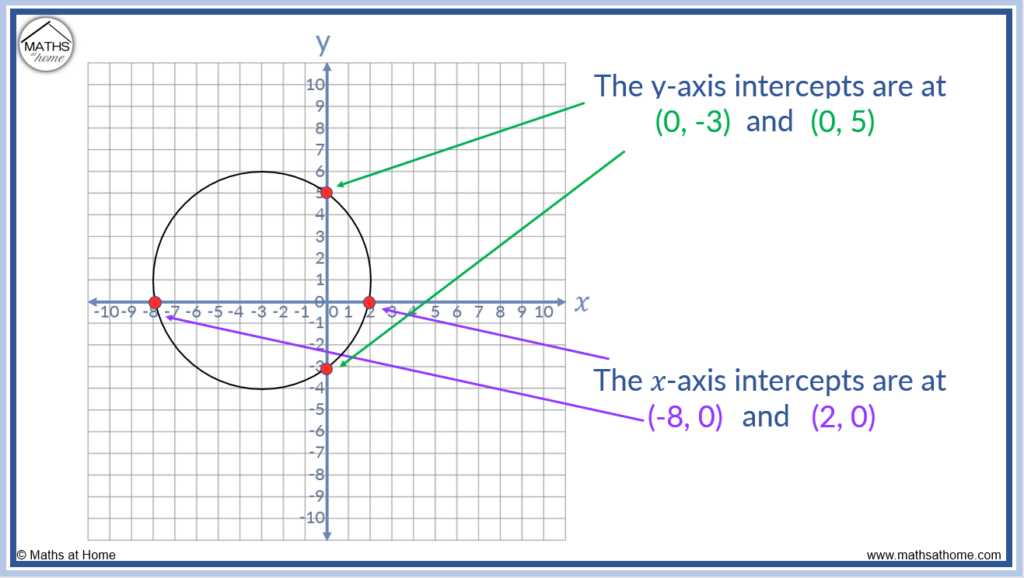
On the circle shown above, the y intercepts are marked at (0, -3) and (0, v).
The π₯ intercepts are marked at (-eight, 0) and (2,0).
y intercepts always accept the form (chiliad, 0). They e'er have an π₯ coordinate of 0.
π₯ intercepts always take the course (0, k). They always have a y coordinate of 0.
How to Graph A Line using x and y Intercepts
To graph a line using x and y intercepts:
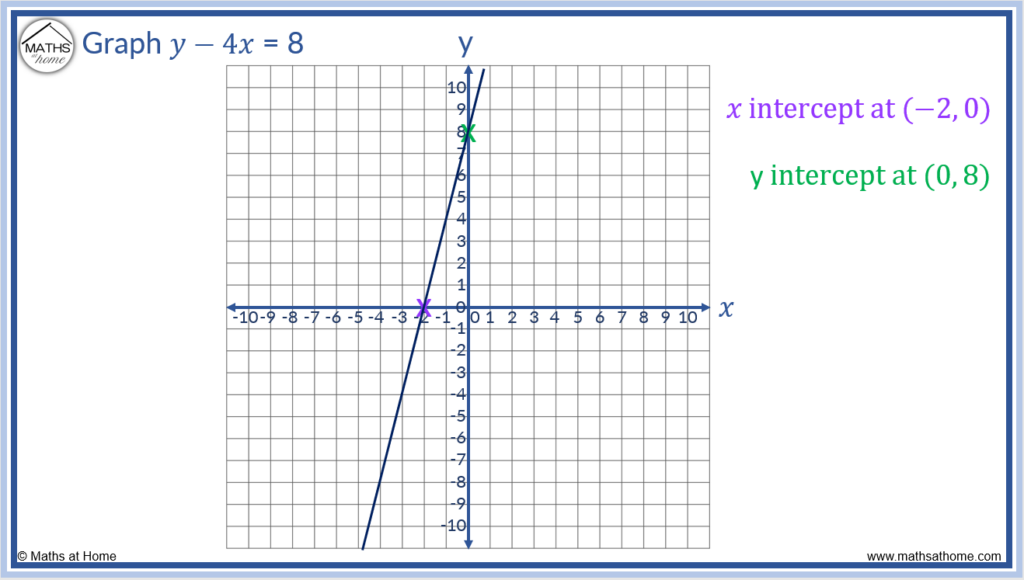
For example, graph the linear function of y – 4π₯ = 8.
Footstep 1. Substitute π₯ = 0 into the equation to discover the y-intercept
When π₯ = 0, the equation y – 4π₯ = 8 becomes y = 8.
The y-intercept is therefore (0, 8)
Step 2. Substitute y = 0 into the equation to discover the π₯-intercept
When y = 0, the equation y – 4π₯ = 8 becomes -4π₯ = viii.
Dividing both sides by -iv, nosotros become π₯ = -2.
The π₯-intercept is therefore (-2, 0)
Stride 3. Connect these 2 intercepts with a directly line
The two intercepts are plotted at (-2, 0) and (0, 8).
A straight line is then drawn between these two points to complete the graph.
For example, the equation 3y + 3π₯ =6 is written in standard form. Find the π₯ and y intercepts.
Here A = 3, B = three and C = 6.
Setting π₯ = 0, the equation 3y + 3π₯ = vi becomes 3y = half-dozen and so the y-intercept is y = two.
The coordinate of the y intercept is (0, 2).
We can come across that C/B becomes 6/three which equals 2.
Setting y = 0, the equation 3y + threeπ₯ = 6 becomes 3π₯ = vi and then, the π₯-intercept is π₯ = 2.
The coordinate of the π₯ intercept is (two, 0)
We tin can see that C/A becomes 6/3 which equals 2.
This standard form equation can now be graphed by plotting these two intercept coordinates and drawing a line between them.
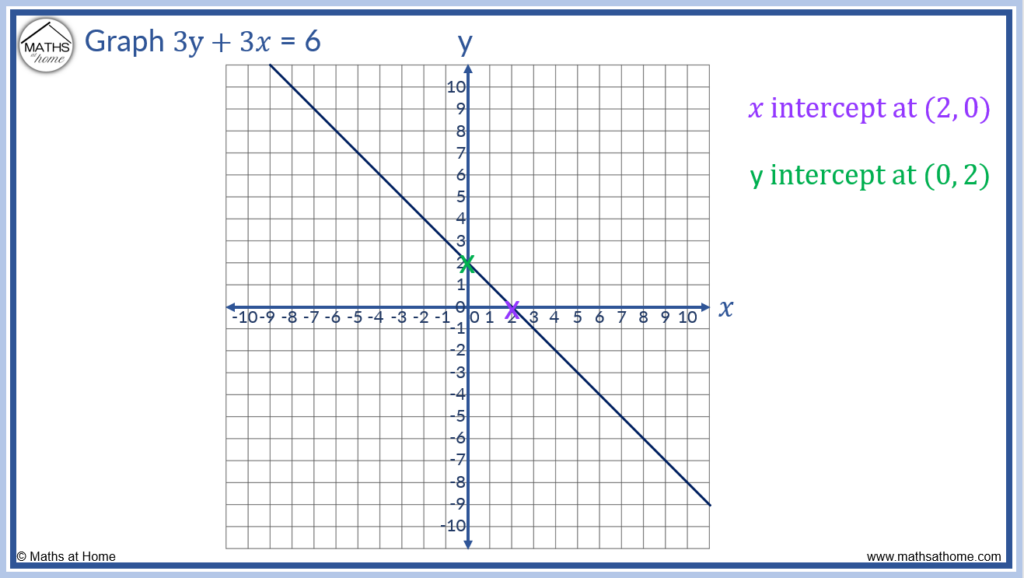
If the π₯ and y axis intercepts are the aforementioned, the line has a gradient of -1. For every one unit right, the line travels one unit downwards.
Finding the π₯ and y Intercepts with Fractions
To find the π₯ intercept, substitute y=0 into the equation and solve for π₯. To find the y intercept, substitute π₯ = 0 into the equation and solve for y. If there is a fraction following the exchange, multiply each term past the denominator and split up each term by the numerator to solve it.
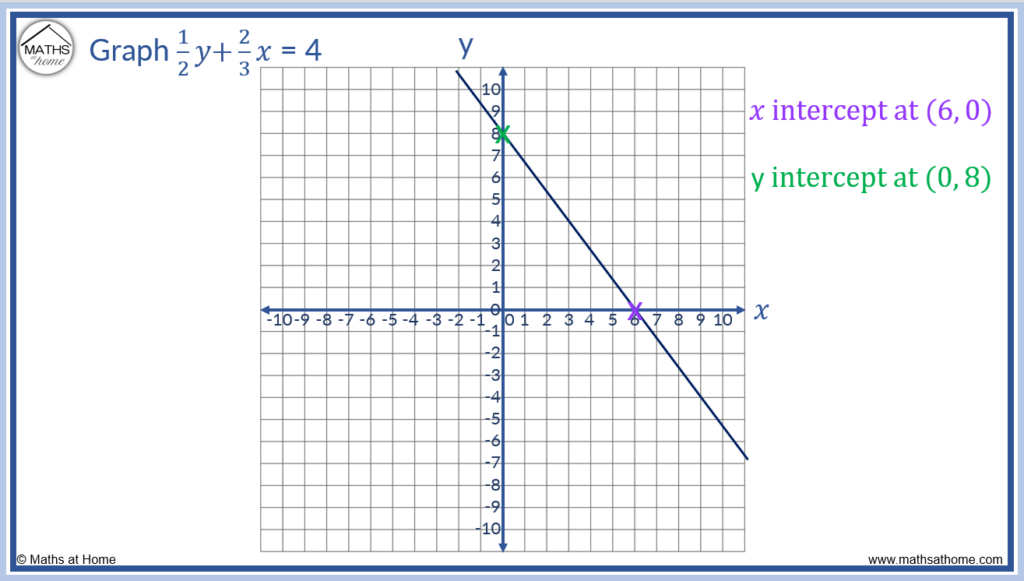
For instance, detect the π₯ and y intercepts of .
To discover the π₯ intercept, substitute y = 0 and solve for π₯.
This results in . Since there is a fraction, multiply by the denominator and then dissever by the numerator.
Multiplying both sides of the equation by 3, the equation becomes 2π₯ = 12.
So dividing both sides of the equation past 2, π₯ = six.
Therefore the π₯ intercept is constitute at (six, 0).
To observe the y intercept, substitute π₯ = 0 and solve for y.
This results in . To notice the intercept of this fractional equation, multiply both sides of the equation by the denominator of 2.
This results in 2y = viii.
Therefore the y intercept of this equation is (0, 8).
The line can be graphed by plotting the intercepts and cartoon a line betwixt them,
How to Find π₯ and y Intercepts for a Linear Part
A linear equation is written in the form y = mx + b. b is the constant term and is the value of the y-intercept. The x-intercept is the value of x when y = 0. For a linear function, the 10-intercept is equal to -b/m. For case, y = 2x – 6 has a y-intercept of -6 and an x-intercept of 3.
In linear equations of the form, y = mπ₯ + b, the value of thousand is the coefficient of π₯ and b is the constant term. This means that thou is the value π₯ is multiplied by and b is the number on its ain.
When written in slope-intercept grade, the equation of a directly line is y = mπ₯ + b.
To find the π₯ intercept, set y = 0 and solve for x.
y = grandπ₯ + b becomes 0 = thousandπ₯ + b.
We can rearrange this for π₯ to go π₯ = -b/yard.
To detect the y intercept, substitute π₯ = 0 and solve for y.
y = kπ₯ + b becomes y = b.
For instance, in the equation y = 2π₯ – half dozen, m = 2 and b = -6.
Therefore the y-axis intercept is b, which is -6. The y intercept is at (0, -6).
The π₯-axis intercept is -b/m, which is 6/2 which is three. The π₯ intercept is at (iii, 0).
The aforementioned results for the π₯ and y intercepts tin be establish by substituting y = 0 and π₯ = 0 respectively into the equation y = iiπ₯ – vi.
Finding π₯ and y Intercepts for Rational Functions
To find the 10-axis intercept of a rational function, substitute y = 0 and solve for x. The x-axis intercept is therefore institute when the numerator of the rational office equals nil. The y-centrality intercept is institute by substituting 10 = 0 into the function and evaluating the effect.
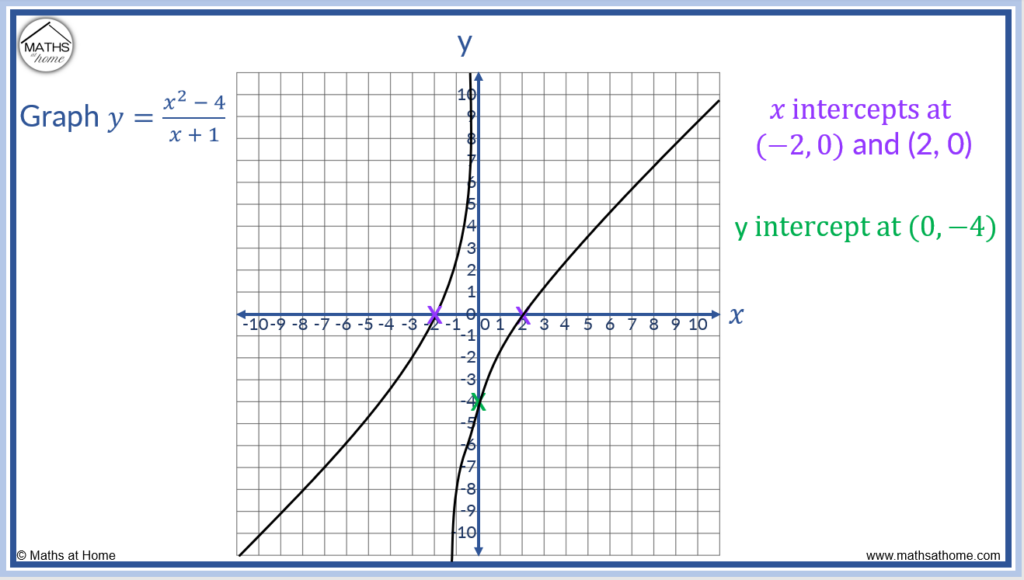
For example, notice the π₯ and y intercepts for .
To find the π₯-axis intercept, fix y = 0.
becomes
.
Nosotros tin can multiply both sides of the equation past π₯ + ane to get . We can skip to this part of the solution when we are finding the π₯ intercept of a rational function.
Simply set the numerator equal to zero.
Therefore 0 = (π₯+two)(π₯-two).
Setting each subclass equal to zero, the solutions become π₯ = -two and π₯ = 2.
The π₯-intercepts are (-two, 0) and (2, 0).
To find the y-centrality intercept, substitute π₯ = 0 into the office.
becomes
which becomes
.
y = -iv and so, the y-axis intercept is (0, -4).
Finding π₯ and y Intercepts for a Parabola
A parabola of the course y = ax2 + bx + c has only i y-axis intercept at (0, c). The parabola can accept upwardly to two x-axis intercepts which are its roots or zeros. To notice the ten-centrality intercepts, fix y = 0 and solve the quadratic equation using the quadratic formula or past factorisation.
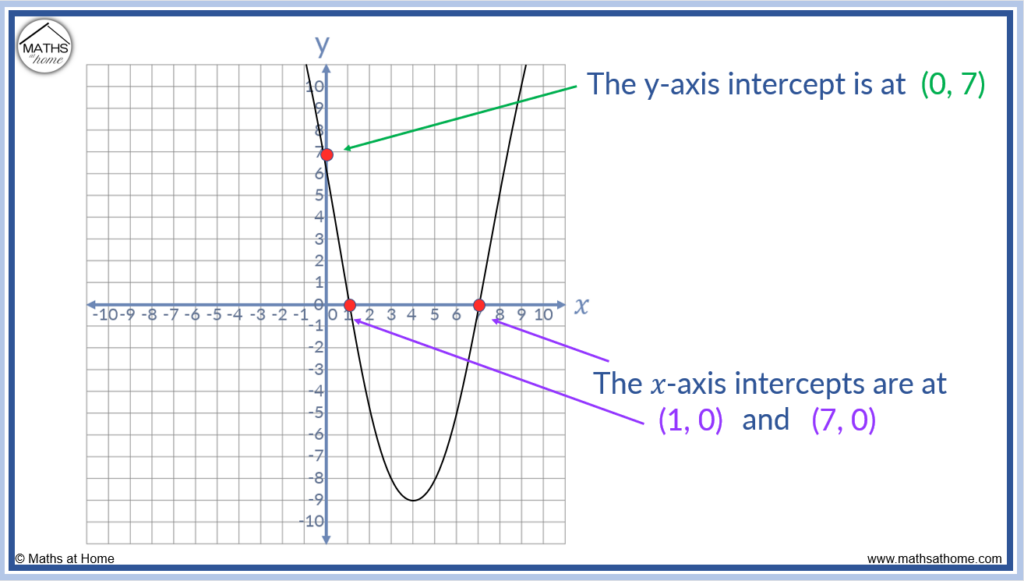
For example, find the π₯ and y intercepts of y = π₯2 – 8x + seven.
The y-intercept can be found by substituting π₯ = 0 into the equation. This results in y = 7.
More than merely, the y-intercept is at (0, c). In the equation y = π₯2 – 8x + 7, the value of c is vii. Therefore the y-centrality intercept is at (0, 7).
To find the π₯-axis intercepts, we set y = 0 and solve for π₯.
y = π₯2 – 8x + 7 becomes 0 = π₯2 – 8x + vii. We can factorise the equation to get (π₯ – i)(π₯ – seven) = 0.
Therefore, setting each bracket to equal 0, the solutions are π₯ = one and π₯ = 7. Therefore the π₯-axis intercepts are at (i, 0) and (7,0).
The quadratic formula can be used to notice the π₯-axis intercepts of any parabola.
The quadratic formula tells us that . This means that the first π₯-axis intercept is found at
and the 2d π₯-axis intercept is found at
.
For the equation y = π₯2 – 8x + 7: a = 1, b = -8 and c = vii.
The quadratic formula, becomes
, which simplifies to
, which results in π₯ = 1 and π₯ = 7.
For any quadratic part, the axis of symmetry is found exactly in between the π₯-centrality intercepts. To find the axis of symmetry using the π₯-intercepts, merely add the π₯ coordinates of each π₯-axis intercept and then divide this result by 2.
The 2 π₯ intercepts are at π₯ = i and π₯ = 7. Adding 1 and 7 and so dividing past 2 gives u.s.a. π₯ = 4.
The equation of the axis of symmetry is π₯ = iv.
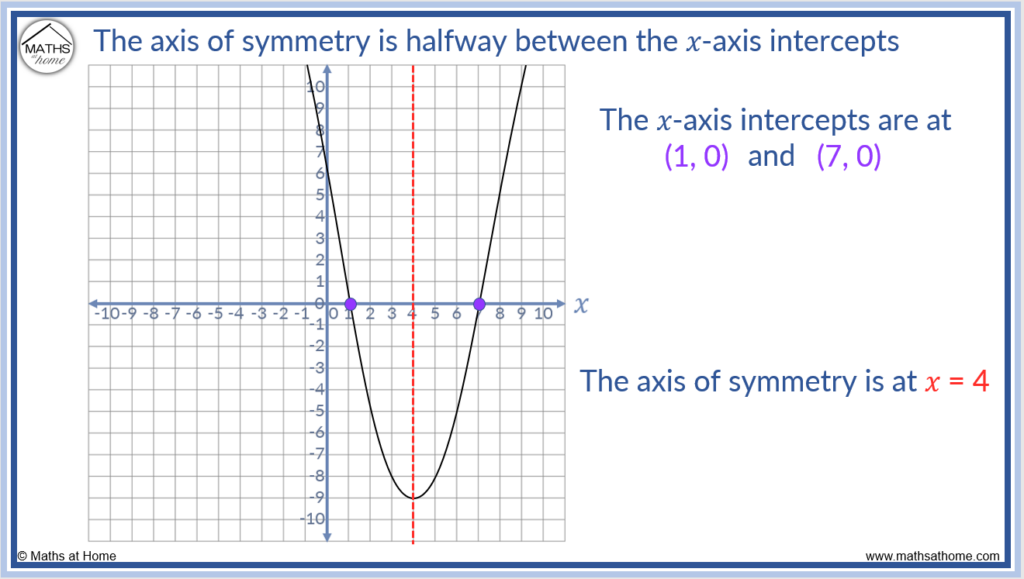
The vertex is the turning betoken of a quadratic graph. The vertex of whatsoever quadratic, aπ₯ii + bπ₯ + c lies on its axis of symmetry.
Therefore the π₯ coordinate of the vertex is e'er exactly halfway betwixt the two π₯-axis intercepts of the quadratic at . The y coordinate of the vertex can so be found by substituting this value of π₯ into the original quadratic role.
For the equation, y = π₯2 – 8x + 7, the equation for the π₯ coordinate of the vertex becomes
. This equals π₯ = 4.
This means that the π₯ coordinate of the vertex is 4.
To find the y coordinate of the vertex, simply substitute the π₯ coordinate of the vertex into the original quadratic equation.
π₯2 – 8x + vii is equal to -9 when π₯ = 4.
Therefore the coordinates of the vertex are (4, -9).
Finding π₯ and y Intercepts for a Circumvolve
To find the x-intercepts of a circle, substitute y = 0 and solve the resulting quadratic for ten. To find the y-intercepts of a circumvolve, substitute x = 0 and solve the resulting quadratic for y. A circle may have 0, 1 or 2 x-centrality or y-axis intercepts depending on the number of solutions to the quadratic.
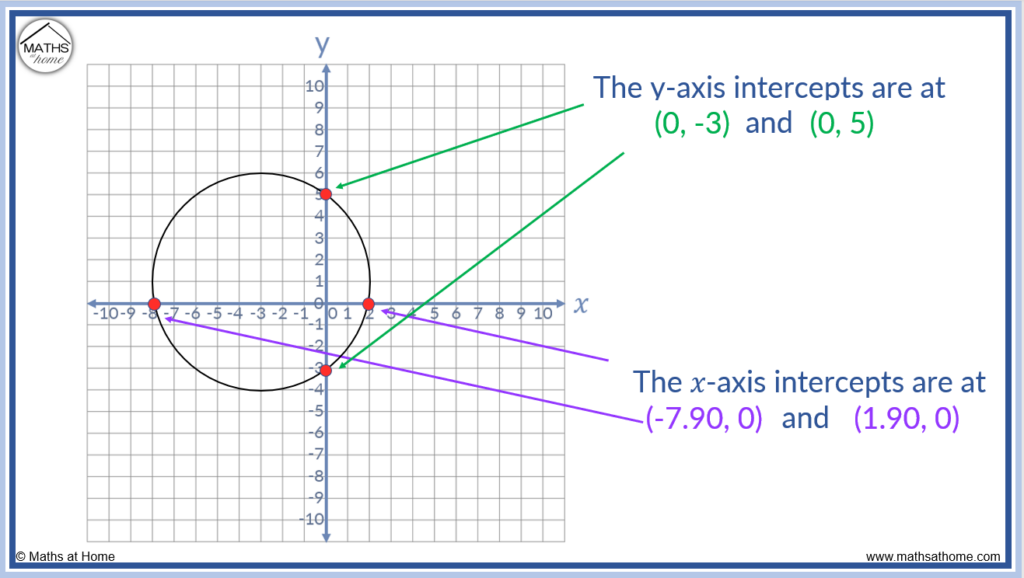
For case, detect the π₯ and y intercepts of (π₯+3)2 + (y-i)2 = 25.
To find the π₯ intercept, substitute y = 0 to get (π₯+iii)2 + (0-i)two = 25.
This becomes (π₯+three)(π₯+3) + (-1)2 = 25.
Expanding this, we get π₯2 + 6π₯ + nine + 1 = 25. We ready a quadratic equation equal to nil to solve it.
Nosotros get π₯two + 6π₯ – 15 = 0. This cannot exist factorised but solving this with the quadratic formula we get π₯ = -vii.xc or π₯ = one.90.
To find the y intercepts of a circle, set up π₯ = 0 and solve the resulting quadratic equation for y.
(π₯+iii)2 + (y-one)two = 25 becomes (0+iii)2 + (y-one)2 = 25.
This becomes (3)two + (y-ane)(y-1) = 25 which can be expanded to get ix + y2 – 2y + 1 = 25.
Setting this quadratic equation equal to zilch, we get y2 – 2y – 15 = 0.
This can be factorised to get (y-5)(y+iii) = 0, which gives us the solutions of y =5 or y = -iii.
These π₯ and y intercepts are shown on the graph of the circle below.
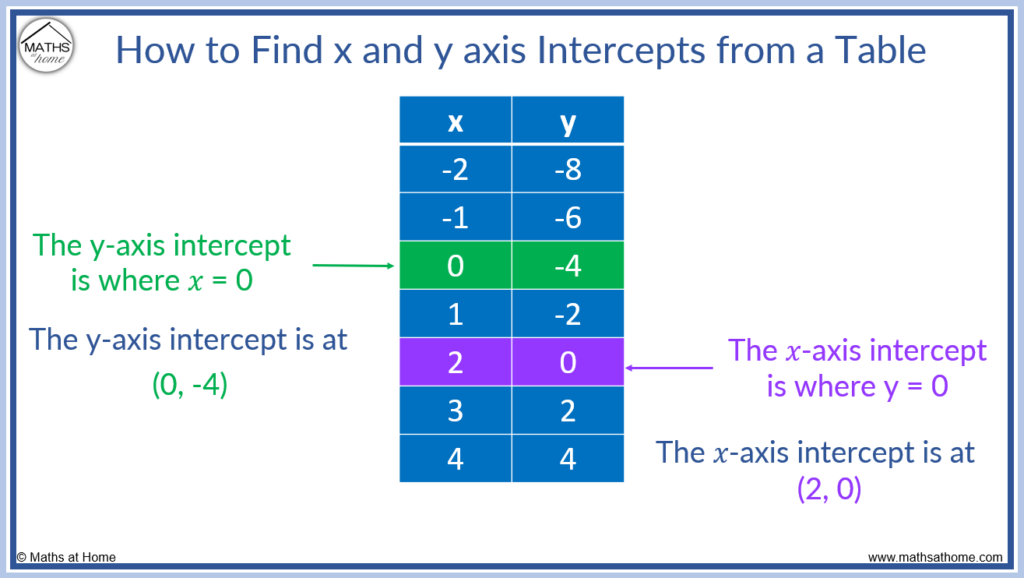
π₯ and y Intercepts From a Table
A table of x and y values make up pairs of coordinates. The 10-intercept is found from the row in the tabular array with a y coordinate of 0. The y-intercept is establish from the row in the table with an x coordinate of 0.
The table below shows the table of coordinates formed from the role y = 2π₯ – 4.
The y-centrality intercept is seen to be (0, -iv). This is the but pair of coordinates that have an π₯ value of 0.
The π₯-axis intercept is seen to be (2, 0). This is the merely pair of coordinates that have a y value of 0.
How to Find the x and y Intercepts from 2 Points
To observe the x and y intercepts from two points, offset notice the equation of the line. The x intercept can be found past substituting y = 0 into the equation of the line. The y intercept can be found past substituting x = 0 into the equation of the line.
Finding the y Intercept From 2 Points
To observe the y intercept from 2 points:
For example, find the y intercept of the line passing through (2, three) and (four, nine).
Step 1. Find the slope past dividing the modify in y coordinates by the change in x coordinates.
Between the y coordinates of three and 9 in that location is a change of +half dozen.
Between the x coordinates of 2 and four there is a change of +two.
6 ÷ ii = 3 so the gradient = 3.
Pace 2. Substitute the gradient, chiliad into the equation y = mx + c along with the x and y values of one of the coordinates.
Nosotros call the gradient 1000. Therefore as calculated in step 1, m = three.
We at present select the ten and y values from either coordinate. Nosotros volition choose (two, iii) then ten = 2 and y = 3.
Substituting m = 3, x = two and y = 3 into y = mx + c,
we get 3 = 6 + c.
Step 3. Apply these values to work out c, the y-intercept.
Since three = 6 + c, the value of c = -3.
Therefore the y intercept is y = -3.
The y-intercept is (0, -3).
Finding the x Intercept from 2 Points
To find the ten intercept from 2 points:
Pace i. Observe the equation of the line using the ii points.
As seen in the steps above, the equation of the line is y = 3x – 3.
Pace ii. Substitute y=0 into the equation of the line.
y = 3x – 3 becomes 0 = 3x – iii.
Footstep 3. Solve the resulting equation for x.
0 = 3x – 3 can be solved by adding 3 to both sides.
3 = 3x
Nosotros divide both sides by 3 to become ten = one.
The ten intercept is plant at (1, 0).
Y Mx B X Intercept,
Source: https://mathsathome.com/x-and-y-intercepts/
Posted by: germanhaing1965.blogspot.com
0 Response to "Y Mx B X Intercept"
Post a Comment